This page is for those who would like to know more about the physics behind climate science. As will be clear from the first three pages there is a lot of basic physics behind our understanding of Earth's climate. This page is in addition to the material in the other pages, so be sure to have worked through those pages before coming here. It should be particularly helpful to students at senior secondary levels. While it has been written particularly with the new Victorian VCE Physics curriculum in mind, it should help anyone curious about climate change to gain an understanding of the basic science.
1. Electromagnetic radiation and light
Earth’s climate is fundamentally the result of a balance between incoming energy from the Sun (largely visible light) and outgoing energy in the form of long wavelength radiation. Indeed, both the incoming and outgoing energy are in the form of electromagnetic radiation. So the first step in understanding climate science is to gain a little understanding of the nature of electromagnetic radiation.
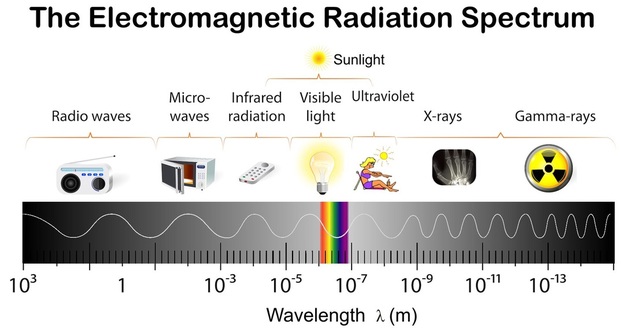
As you can see in this diagram, electromagnetic waves include radio waves, microwaves, invisible infrared, the visible 'rainbow' colours, ultraviolet, x-rays and gamma rays. All of them are generated by accelerating electric charges: Radio waves by electric currents flowing back and forth in antenna, infrared, visible and ultraviolet by electrons in atoms, and x and gamma rays by high energy collisions of nuclei.
They are basically waves of electric and magnetic fields ranging from many metres long (radio) to well under a trillionth of a metre. Visible light waves are around half a micrometre (0.5 µm, a µm is one millionth of a metre)
They are basically waves of electric and magnetic fields ranging from many metres long (radio) to well under a trillionth of a metre. Visible light waves are around half a micrometre (0.5 µm, a µm is one millionth of a metre)
The atoms in any solid material above absolute zero (–273ºC or 0 K, K standing for Kelvin, the temperature scale starting from absolute zero, and one K degree also 1 ºC) possess various forms of energy. The higher the temperature the greater the energy. Some of this energy goes to the electrons around the atoms which tend to lose it by giving off electromagnetic radiation. The wavelength of this radiation depends on how much energy is lost – the greater the energy lost the shorter the wavelength. This radiation is mostly in the form of infrared (what you feel from a radiator) but once the object is hot enough (an incandescent light bulb for example) the radiation starts to include the visible part of the spectrum.
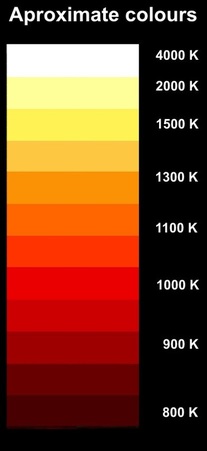
We sometimes call this sort of radiation 'black-body radiation', the idea being that an ideal black body only gives off this electromagnetic radiation and nothing else. (A brightly painted object reflects lots of colours from other sources, so it's not an ideal 'black-body'.) At ordinary temperatures the radiation from a black-body (BB) is entirely infrared, but as the temperature increases it starts to become visible - first deep red then getting whiter, and even bluer if very hot. This chart shows the approximate relationship between colours and absolute temperatures (degrees Kelvin) for an ideal BB. Once they start glowing, almost any object is near to an ideal BB. In fact, experienced kiln operators can tell the temperature of their kiln simply from its colour. (Note, 1000 K = 727ºC) The temperature of the Sun's surface is about 5800K and that's pretty much what we call white. Once the temperature goes beyond about 6000 K the colour starts to look bluish. Some stars look bluish because they are extremely hot. Sirius, for example, looks quite a bluish white because it has a surface temperature of about 9,400 K.
We sometimes call this sort of radiation 'black-body radiation', the idea being that an ideal black body only gives off this electromagnetic radiation and nothing else. (A brightly painted object reflects lots of colours from other sources, so it's not an ideal 'black-body'.) At ordinary temperatures the radiation from a black-body (BB) is entirely infrared, but as the temperature increases it starts to become visible - first deep red then getting whiter, and even bluer if very hot. This chart shows the approximate relationship between colours and absolute temperatures (degrees Kelvin) for an ideal BB. Once they start glowing, almost any object is near to an ideal BB. In fact, experienced kiln operators can tell the temperature of their kiln simply from its colour. (Note, 1000 K = 727ºC) The temperature of the Sun's surface is about 5800K and that's pretty much what we call white. Once the temperature goes beyond about 6000 K the colour starts to look bluish. Some stars look bluish because they are extremely hot. Sirius, for example, looks quite a bluish white because it has a surface temperature of about 9,400 K.
Clearly there is some serious physics involved in the relationship between the temperature of an object and the nature of its radiation! We will have a look at a little of it now, in as far as it relates to the Earth's energy balance. There are two important laws of physics which relate to the emission of radiation from a hot (or even cold) object. They are actually two aspects of the one bit of physics. Fourier used earlier versions of these laws to predict that the Earth should be a frozen snowball if not for the greenhouse effect (as we saw on the Climate 1 page). One of these laws deals with the total amount of radiation emitted from a hot body and the other tells us about the nature of that radiation.

The first of these laws is called the Stefan-Boltzman equation and was discovered by those two Austrian physicists in 1879. Briefly, it tells us that the total amount of power radiated from any object depends on three things: the total surface area of the object, how well the surface emits radiation, and the temperature. They put it together this way: P = eσAT^4 where
P is the total power radiated in watts,
e is the emissivity which varies from 0 to 1 depending on how well the surface emits. An ideal ‘black-body’ would have a value of e = 1, whereas a shiny surface would have a much lower value.
σ is what’s known as the Stefan-Boltzman constant, which has the value shown in SI units.
A is the area in square metres
T^4 is the fourth power of the temperature in Kelvin
Clearly, as the temperature increases the amount of radiation increases very quickly. If the temperature doubles, the amount of radiation will go up by 2 to the fourth power, which is 16 times.
This equation enables us to work out the total energy radiated by any body at a particular temperature. Basically, what Fourier did was to use this idea to find the temperature at which the Earth would need to be in order to radiate away all the energy it received from the Sun - and hence remain at an equilibrium temperature.
P is the total power radiated in watts,
e is the emissivity which varies from 0 to 1 depending on how well the surface emits. An ideal ‘black-body’ would have a value of e = 1, whereas a shiny surface would have a much lower value.
σ is what’s known as the Stefan-Boltzman constant, which has the value shown in SI units.
A is the area in square metres
T^4 is the fourth power of the temperature in Kelvin
Clearly, as the temperature increases the amount of radiation increases very quickly. If the temperature doubles, the amount of radiation will go up by 2 to the fourth power, which is 16 times.
This equation enables us to work out the total energy radiated by any body at a particular temperature. Basically, what Fourier did was to use this idea to find the temperature at which the Earth would need to be in order to radiate away all the energy it received from the Sun - and hence remain at an equilibrium temperature.
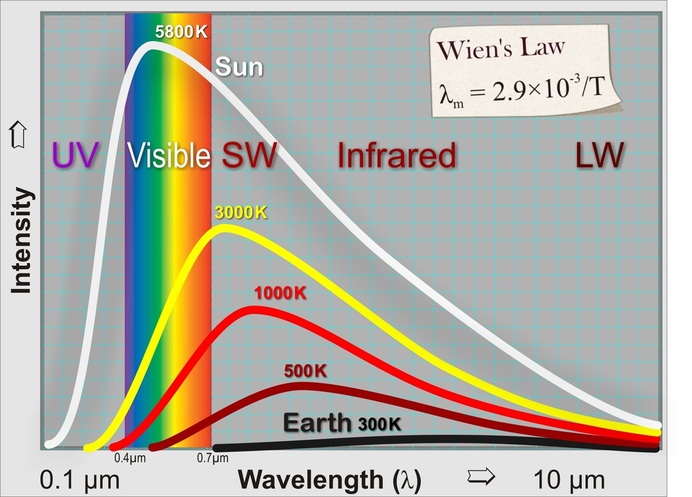
The second of these laws was discovered back in the 1890's by Wilhelm Wien. He figured out the relationship between the wavelength of electromagnetic radiation and the temperature of the body emitting it. The relationship is illustrated graphically in this diagram (not strictly to scale). The energy is spread over a spectrum of wavelengths spread either side of a peak. The peak wavelength is referred to as λm. λ is the symbol for 'wavelength' and λm stands for 'wavelength maximum'. Wien found that the peak wavelength is inversely proportional to the temperature by this simple equation:
λm = 2.9×10‾³/T
where the peak wavelength λm is in metres and the temperature in Kelvin. This relationship is now known as 'Wien's Law'. As you can see, the Earth, which is roughly 300 K has a peak wavelength about 10 µm (1 µm is one millionth of a metre) which is in the long infrared, and of course is completely invisible to us. On the other hand the Sun, at 5800 K has a peak wavelength of 0.5 µm which is in the blue/green part of the spectrum.
λm = 2.9×10‾³/T
where the peak wavelength λm is in metres and the temperature in Kelvin. This relationship is now known as 'Wien's Law'. As you can see, the Earth, which is roughly 300 K has a peak wavelength about 10 µm (1 µm is one millionth of a metre) which is in the long infrared, and of course is completely invisible to us. On the other hand the Sun, at 5800 K has a peak wavelength of 0.5 µm which is in the blue/green part of the spectrum.
The light we see from the Sun clearly contains a spread of colours across the spectrum. We see this combination as 'white'. However, what is important in our present study is the total amount of energy emitted by the Sun and absorbed by the Earth, and then re-emitted by the Earth. You can see that the energy emitted by the Sun, although mostly in the infrared (IR) contains a considerable amount of visible light as well as UV (which is what gives us sunburn!). On the other hand, the radiation emitted by the Earth is entirely in the long wavelength IR part of the spectrum. As explained on the 'Climate 1' page, it is the balance between the short wavelength IR and visible radiation absorbed from the Sun and the long wavelength IR re-emitted by the Earth that determines the Earth's climate.
Now if the atmosphere was as transparent to infrared radiation as it is to visible light it would be a simple enough physics problem to work out at what temperature the Earth would have to be to balance the incoming and outgoing radiation. This is what Fourier did back in the 1800's. He got a temperature of about minus 15 degrees. Something like 30 degrees too low! The explanation, of course, is that the atmosphere is NOT transparent to a lot of the infrared part of the spectrum. The atmosphere absorbs it and thus acts a little like a blanket, keeping heat in and warming the Earth. This is the so called 'Greenhouse effect' which is all important in our discussion of 'global warming'. Basically, the problem is that we are increasing the thickness of this 'blanket'. To find out how and why we need to delve a little further into the physics of it all.
Now if the atmosphere was as transparent to infrared radiation as it is to visible light it would be a simple enough physics problem to work out at what temperature the Earth would have to be to balance the incoming and outgoing radiation. This is what Fourier did back in the 1800's. He got a temperature of about minus 15 degrees. Something like 30 degrees too low! The explanation, of course, is that the atmosphere is NOT transparent to a lot of the infrared part of the spectrum. The atmosphere absorbs it and thus acts a little like a blanket, keeping heat in and warming the Earth. This is the so called 'Greenhouse effect' which is all important in our discussion of 'global warming'. Basically, the problem is that we are increasing the thickness of this 'blanket'. To find out how and why we need to delve a little further into the physics of it all.
2. The atmosphere and Earth's energy balance
There are two more important laws of physics involved in figuring out the Earth's climate. The first law of thermodynamics is what is often simply called the law of conservation of energy - that it, energy can not be created or destroyed. In our context, that means that for the Earth to be in equilibrium, all the energy coming in from the Sun must be equal to that going out. At present that is not the case, and so energy is building up. (More on this below.) The second law of thermodynamics is more complicated. It says that 'entropy' must always increase. What that means, in simple terms, is that disorder will increase unless energy is used to make order. Think - what happens to your room until you decide to put some energy into tidying it up! In the system of the Earth's climate, if left to itself it would all just go to an even temperature with no differences. Storms are an example of where this does NOT happen. Of course the climate system is not being 'left to itself'. The Sun is putting energy into it all the time. Energy flows into the storms and gives them order. The physics of putting all that together is, needless to say, rather complicated and beyond the scope of our present considerations!
The balance between the incoming and outgoing radiation energy is the basic determinant of the Earth's climate. An imbalance will result in either a heating up or cooling down which in turn determines factors such as the amount of ice at the poles and the strength of weather events (which are driven by ocean heat). For this reason, scientists have put a lot of effort into trying to carefully measure and understand both the Earth's incoming and outgoing radiation energy. While the incoming energy is basically just that coming from the Sun minus that reflected by clouds and earth, the outgoing is more complicated because of the absorption of IR by the atmosphere. We will look at some of the physics behind that absorption now.
The balance between the incoming and outgoing radiation energy is the basic determinant of the Earth's climate. An imbalance will result in either a heating up or cooling down which in turn determines factors such as the amount of ice at the poles and the strength of weather events (which are driven by ocean heat). For this reason, scientists have put a lot of effort into trying to carefully measure and understand both the Earth's incoming and outgoing radiation energy. While the incoming energy is basically just that coming from the Sun minus that reflected by clouds and earth, the outgoing is more complicated because of the absorption of IR by the atmosphere. We will look at some of the physics behind that absorption now.
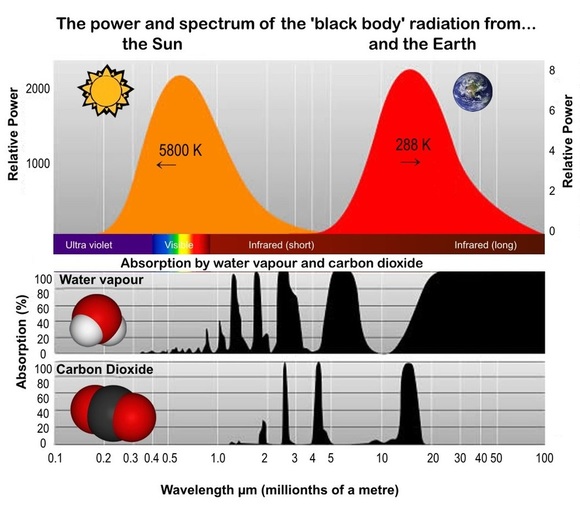
As was pointed out on the Climate 1 page, back in the 1860's John Tyndall discovered that it was the carbon dioxide and the water vapour in the atmosphere that were absorbing the long wavelength infrared radiation. We now have much better ways to measure this absorption and this diagram shows the spectrum of the emitted radiation as well as the relative wavelengths of infrared that are absorbed by each gas (lower black shapes). Notice that while H2O absorbs the high and low parts of the Earth's radiation spectrum, CO2 has a strong absorption peak at the peak radiation.
Why do H2O and CO2 absorb this IR radiation while oxygen (O2) and nitrogen (N2) don't? You might notice a difference in the symbols (hence the molecules) of those four gases. Yes, CO2 and H2O contain three atoms while N2 and O2 only contain two. Very simply, the two atom molecules are more rigid than the three atom molecules. This means it takes more energy to 'disturb' the O2 and N2 molecules. It turns out that the IR light just doesn't have enough to disturb (and therefore get absorbed by) O2 and N2, but it does have enough to interact with the CO2 and H2O because they are less rigid and can take on smaller amounts of energy. This is all to do with the energy of light 'photons' - you will find out more in your further studies!
Why do H2O and CO2 absorb this IR radiation while oxygen (O2) and nitrogen (N2) don't? You might notice a difference in the symbols (hence the molecules) of those four gases. Yes, CO2 and H2O contain three atoms while N2 and O2 only contain two. Very simply, the two atom molecules are more rigid than the three atom molecules. This means it takes more energy to 'disturb' the O2 and N2 molecules. It turns out that the IR light just doesn't have enough to disturb (and therefore get absorbed by) O2 and N2, but it does have enough to interact with the CO2 and H2O because they are less rigid and can take on smaller amounts of energy. This is all to do with the energy of light 'photons' - you will find out more in your further studies!
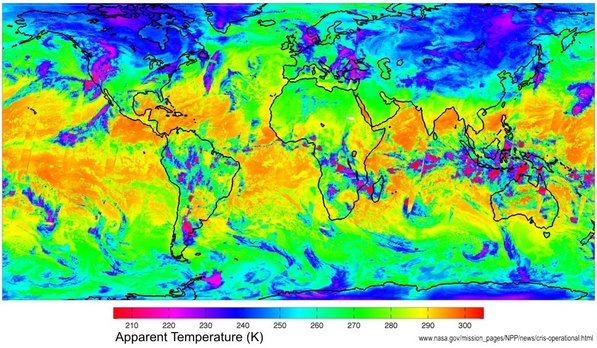
The radiation that actually leaves the Earth is therefore what is emitted (the red in the diagram above) minus that absorbed by the atmosphere. Of course the Earth is not at a uniform temperature of 288 K as suggested by that diagram (288 K is the average). It varies from very cold near the poles to much hotter around the equator. However, the total radiation energy coming from the Earth can be measured by satellites equipped with special infrared detectors. The diagram at right, from NASA, gives a visual impression of the sort of data these satellites collect. It shows the 'apparent temperature' of the Earth (as seen from space) over three days in 2012. This enables scientists to calculate the total energy escaping from the Earth. This can then be compared to that being absorbed by the Earth (from the Sun). The difference, if any, is the Earth's energy 'imbalance'. In fact scientists have now been able to calculate most of these energy flows fairly well - and calculate the imbalance! Let's have a look at the numbers:
3. Putting the numbers together

This diagram, from NASA (2014) shows the energy flows in the Earth's climate system. The numbers are the power in watts per square metre of the Earth's surface. The yellow arrows represent the energy from the Sun absorbed and reflected. After subtracting the reflected radiation energy from the incoming we find the total absorbed radiation to be 240.5 watts per square metre.
The outgoing radiation is somewhat more complicated. You can see that the total emitted is 398.2, but a lot of this is absorbed by the greenhouse gases in the atmosphere and re-emitted back to the Earth. Notice that the 'greenhouse effect' is big. About 85% of the heat emitted from the Earth is returned. It is not hard to see that without it the Earth would be a frozen snowball! Having already increased the major greenhouse gas by 43% we have to expect more warming. The purple arrows represent non-radiation processes: Thermals are simply the transfer of heat directly by conduction and convection of air. When moisture evaporates from the ocean it absorbs heat. When it condenses to form clouds that 'latent' heat is released again in the clouds.
When all this is taken into account we find that 239.9 watts per square metre of infrared radiation is released to space. This is 0.6 watts less that the 240.5 per square metre total incoming.
It is this extra 0.6 watts of heat energy for every square metre of Earth that is the problem.
The outgoing radiation is somewhat more complicated. You can see that the total emitted is 398.2, but a lot of this is absorbed by the greenhouse gases in the atmosphere and re-emitted back to the Earth. Notice that the 'greenhouse effect' is big. About 85% of the heat emitted from the Earth is returned. It is not hard to see that without it the Earth would be a frozen snowball! Having already increased the major greenhouse gas by 43% we have to expect more warming. The purple arrows represent non-radiation processes: Thermals are simply the transfer of heat directly by conduction and convection of air. When moisture evaporates from the ocean it absorbs heat. When it condenses to form clouds that 'latent' heat is released again in the clouds.
When all this is taken into account we find that 239.9 watts per square metre of infrared radiation is released to space. This is 0.6 watts less that the 240.5 per square metre total incoming.
It is this extra 0.6 watts of heat energy for every square metre of Earth that is the problem.
|
This may not sound like a lot, but the Earth has an awful lot of square metres! Altogether it adds up to a total of about 300 trillion joules of energy every second. But what does a huge number like that actually mean? Well that's almost twenty times the total amount of energy being produced by all human activity around the globe, or about 130 times the total amount of electric power being generated at any time.
[Note: A 'joule' is a unit of energy and a 'watt' is a unit of power, that is, the rate at which energy is used/made. So one 'watt' is one 'joule per second'.] A somewhat more dramatic way of illustrating this huge quantity of extra heat being accumulated in the Earth's climate system is that it is equivalent to the energy output of exploding around 400 Hiroshima sized nuclear bombs EVERY MINUTE all day every day. We note that this figure of 0.6 watts per square metre is not accurately known, as it is the difference between fairly large numbers. The uncertainty is roughly ±0.2 watts. So it might not be quite as bad (0.4 watts) as we think, but equally it might be worse (0.8 watts) |
The calculations above are based on the measurement of incoming and outgoing radiated energy. They show us that the Earth's energy balance is ... well, out of balance - it is gaining energy at the rate of around 300 trillion joules every second. Clearly this is leading to 'global warming'. However, this is just one way of discovering what is happening to the Earth's climate. This doesn't tell us anything about how or why the warming is happening. Just that it is.
Basically, these calculations are simply confirmation of the various other reasons we believe we are warming the Earth. Geological evidence shows that the Earth's climate is sensitive to CO2 levels (as well as other factors of course). The basic physics of infrared radiation and its interaction with CO2 molecules tells us that if we increase the amount of CO2 in the atmosphere it will trap more heat. And of course the various measurements of the temperature of the atmosphere and oceans are all consistent with added greenhouse warming. To try to take all these things into account scientists use powerful computers to 'crunch the numbers'. So let's look at how they go about it. (There is also quite a bit more on computer models on the Climate 1 page.)
Basically, these calculations are simply confirmation of the various other reasons we believe we are warming the Earth. Geological evidence shows that the Earth's climate is sensitive to CO2 levels (as well as other factors of course). The basic physics of infrared radiation and its interaction with CO2 molecules tells us that if we increase the amount of CO2 in the atmosphere it will trap more heat. And of course the various measurements of the temperature of the atmosphere and oceans are all consistent with added greenhouse warming. To try to take all these things into account scientists use powerful computers to 'crunch the numbers'. So let's look at how they go about it. (There is also quite a bit more on computer models on the Climate 1 page.)
4. Computer models
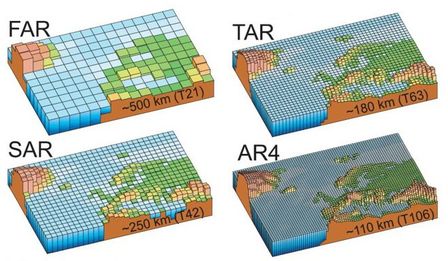
Over the last couple of decades scientists have developed very powerful techniques for calculating how the climate works. The fact that daily forecasts have got a lot better is one indication of this. We can get some idea of how they do this. In order to figure out how the climate works, and therefore how it might change, scientists chop the Earth's atmosphere up into millions of 'cells' about 100 km square and 1 km high. Each cell will be characterised by factors such as temperature, pressure, wind strengths, moisture and more. Clearly if there is a higher temperature or pressure in one cell then clearly heat and wind will flow into adjacent cells. The laws of physics can describe this motion very well. The difference between daily weather forecast models and climate models is that rather than being concerned about specific immediate changes (formation of highs and lows etc.) the climate models work on much longer time scales and respond to long term changes in all sorts of background conditions - such as greenhouse gas levels, volcanic activity, the chemistry of the atmosphere, vegetation changes, ocean circulation and lots more. The diagrams above illustrate the progress in computer modelling over the last couple of decades of IPCC reports as the cell size has reduced giving more accurate results. Abbreviations are for First, Second, Third and 4th Assessment Reports. In the AR5 (2013) the cell sizes are smaller still, around 70 km.

Here are some of the equations that are used to do the calculations. They may look a bit scary, but in fact they express some very basic physics concepts. The first group are known as the Navier-Stokes equations and are actually just an application of Newton's second law (F = ma) to fluid flow in three dimensions. Mass continuity is simply the principle of conservation of mass applied to fluids as they flow with changing density, speed and pressure. The thermodynamics equation is just an expression of the principle of conservation of energy in this context.
It is important to realise that these models apply the well known laws of physics to a physical system. Unlike economic models (which have a very bad record of prediction) they do not involve guesses about human behaviour! Furthermore they can be tested by applying them to past climates to see if they make correct predictions. (See the 'This is where the computer models come in' section on the Climate 1 page for more about models)
It is important to realise that these models apply the well known laws of physics to a physical system. Unlike economic models (which have a very bad record of prediction) they do not involve guesses about human behaviour! Furthermore they can be tested by applying them to past climates to see if they make correct predictions. (See the 'This is where the computer models come in' section on the Climate 1 page for more about models)
